"Science cannot solve the ultimate mystery of nature. And that is because, in the last analysis, we ourselves are part of nature and therefore part of the mystery that we are trying to solve."
- Max Planck -
The Photon
Figure 14a shows what a charged particle (electron) looks like when it is isolated and far away from other particles. But when a free floating electron approaches an atomic nucleus, a transformation takes place. Conventional theory states that the electron is in some kind of orbit around the nucleus. But Foamy Ether Theory states that the electron knot becomes stretched or smeared out across the nucleus. It actually wraps itself around the nucleus, similar to how you would wrap an elastic band around a rolled up map. And just as an elastic band can be wrapped around the map more than once, the electron can also be wrapped around the nucleus more than once. Each extra wrap represents a higher energy level, because the ether from the electron is stretched more tightly.
This explains why the so-called electron orbits only come in discrete levels. In the Rutherford-Bohr atomic model, electrons are only allowed to occupy certain orbits. When an electron jumps from a higher orbit to a lower one, it emits a photon. With Foamy Ether Theory, there are no orbits, just wraps of various quantities and shapes. And of course wraps only come in integer values. To help you visualize this, take a tennis ball and wrap an elastic band around it. That could represent a hydrogen atom. The tennis ball is the nucleus, and the elastic band is the electron. Now wrap the elastic band around the tennis ball two times. This is analogous to a conventional electron absorbing a photon and jumping to a higher orbit. Since the elastic band is now strung more tightly, it contains more energy. Imagine nudging one of the wraps so that it slips off the ball; the elastic band will immediately snap back into one wrap. In Foamy Ether Theory, this results in a photon being emitted because the unwrapping will cause a disturbance in the surrounding ether. And the energy that is lost by going from two wraps to one, is carried away by the photon.
This wrapping and unwrapping, I believe, is the equivalent of David Bohm's enfolding and unfolding order. The enfolding of a wrap is a photon absorption and the unfolding of a wrap is a photon emission.
To demonstrate this, I created three simulations of two particles exchanging a photon. To simplify the picture (and save on CPU time), I used only a one dimensional strand of foamy ether. (This model is very similar to having a long stretched out bungee cord). The first simulation (Figure 17a) is an example where a particle on the right has an electron wrapped around it two times. One wrap (or loop) is let go, which sends a disturbance (wave) in the ether to the particle on the left. I put a pause at the end of the simulation to show that the loop is indeed transfered from one particle to the other. If the particle on the left was in a receiving mode (low energy state), it would capture the loop thereby increasing its loops from two to three. Notice also, that the traveling wave does not look like your typical sine wave. This is not a problem, since no one has actually seen a photon in transit anyway. All we can really do is deduce its wavelength and amplitude when the wave collapses (on a photon detector).
This is how energy is transferred from one atom to another. More wraps makes the ether tighter, hence less stable, which may cause it to unwrap and give off a photon. This unwrapping of 'loops' in ether also explains why light only comes in packets.

Figure 17a

Figure 17b
To further demonstrate how nicely a wrap or loop is transfered from one particle to another, I created a simulation where the particle on the right has a wrap configuration to look like a figure eight (Figure 17c). (Notice that the waveform looks quite different than that of Figure 17a). I put a pause at the end of the simulation to show that the figure eight is indeed transfered from one particle to another.
Foamy Ether Theory can also explain the Pauli Exclusion Principle, which states that no two electrons can occupy the same state or orbit. Using the tennis ball analogy, you can see that no two elastic bands can occupy the same space. Similarly, no ether wraps can occupy the same space.

Figure 17b
Electromagnetic Wave
Figure 18 shows what a typical (conventional) electromagnetic wave may look like in foamy ether. The red line shows where maximum bending takes place; this is also where maximum magnetic field strength occurs. The yellow colored portion shows no bending taking place, therefore no magnetic field.
To figure out the direction of magnetic south, hold your left hand so that your palm is cupped over the red line in Figure 18. Extend your index finger to point to the direction of travel. Extend your thumb and it will be pointing south (away from the diagram in this example).

Direction
of travel
Figure 18
Figure 19 shows how ether distortion, in a traveling wave, causes electric fields to manifest. The ether cells colored in red show bending and compression taking place. Since these cells are increasing in compression, a negative electric field takes place. The green cells indicate where the ether is decreasing its compression (larger cells); this is where a positive electric field takes place. The section in yellow indicates an area of minimum change in compression, therefore minimum electric field strength.

Direction
of travel
Figure 19
Figure 20 shows what a typical photon may look like as it travels through the foamy ether.
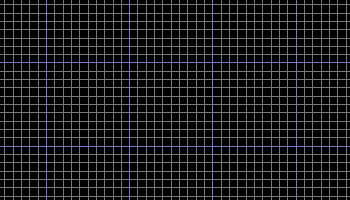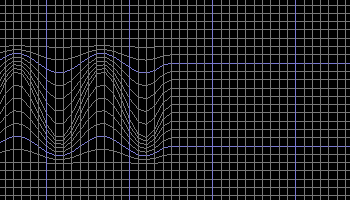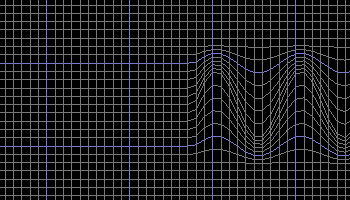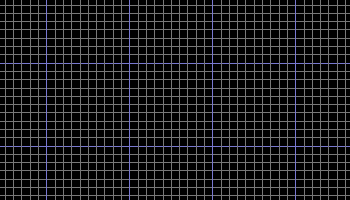
Figure 20
Figure 21 shows how an electromagnetic wave travels in two dimensional foamy ether. This simulation proves that transverse waves are indeed capable of propagating in foamy ether.
Other alternative ether models, that are based on 'ether particles' existing in a liquid or gaseous state, have consistently failed over the years because liquids or gasses are not capable of transmitting transverse waves (where the distortion is perpendicular to the direction of travel).

Figure 21
